Bits & Bytes: A Guide to Low-Level Bit Manipulation

Introduction

Think of bits as the atomic building blocks of computing, they're just 0s and 1s. Bit manipulation is exactly what it sounds like: messing around with these 0s and 1s directly. It's like having a bunch of switches that are either ON or OFF, and we have different ways to play with them - AND, OR, NOT, XOR, and shifting them LEFT or RIGHT. These are the fundamental tools we use when we want to get our hands dirty with low-level programming. The cool thing about bit manipulation is that it's super fast because we're basically talking directly to the computer's processor. The downside? We need to really understand how binary works, and it can get pretty nasty compared to regular high-level programming.

🤔 So... What's The Point?

Well, here's the thing: when we write code, compilers and hardware are already highly optimized for most operations. However, understanding bit manipulation remains valuable because:

It's essential for specific domains like cryptography, encoding/decoding, and game development
It helps implement certain algorithms that work directly with bits
It gives us deeper insight into how computers actually process data

Lastly, a lot of computing stuff feels like magic due to layers of abstractions. Understanding how bits work can help us see beyond the magic of high-level programming and build better systems

Bitwise operations

Bitwise operations are simple rules for manipulating the individual zeros and ones within binary numbers, allowing direct control over data at the fundamental level of computing.

1. AND (`&`)

The bitwise AND operation takes two bit patterns of equal length and performs the logical AND operation on each pair of corresponding bits. The result in each position is 1 if the first bit is 1 and the second bit is 1, otherwise 0. This is the thesame as normal logical operation in a truth system where 0 is represent as false and 1 is represented as true where True AND True = True and False AND True = False

Example:

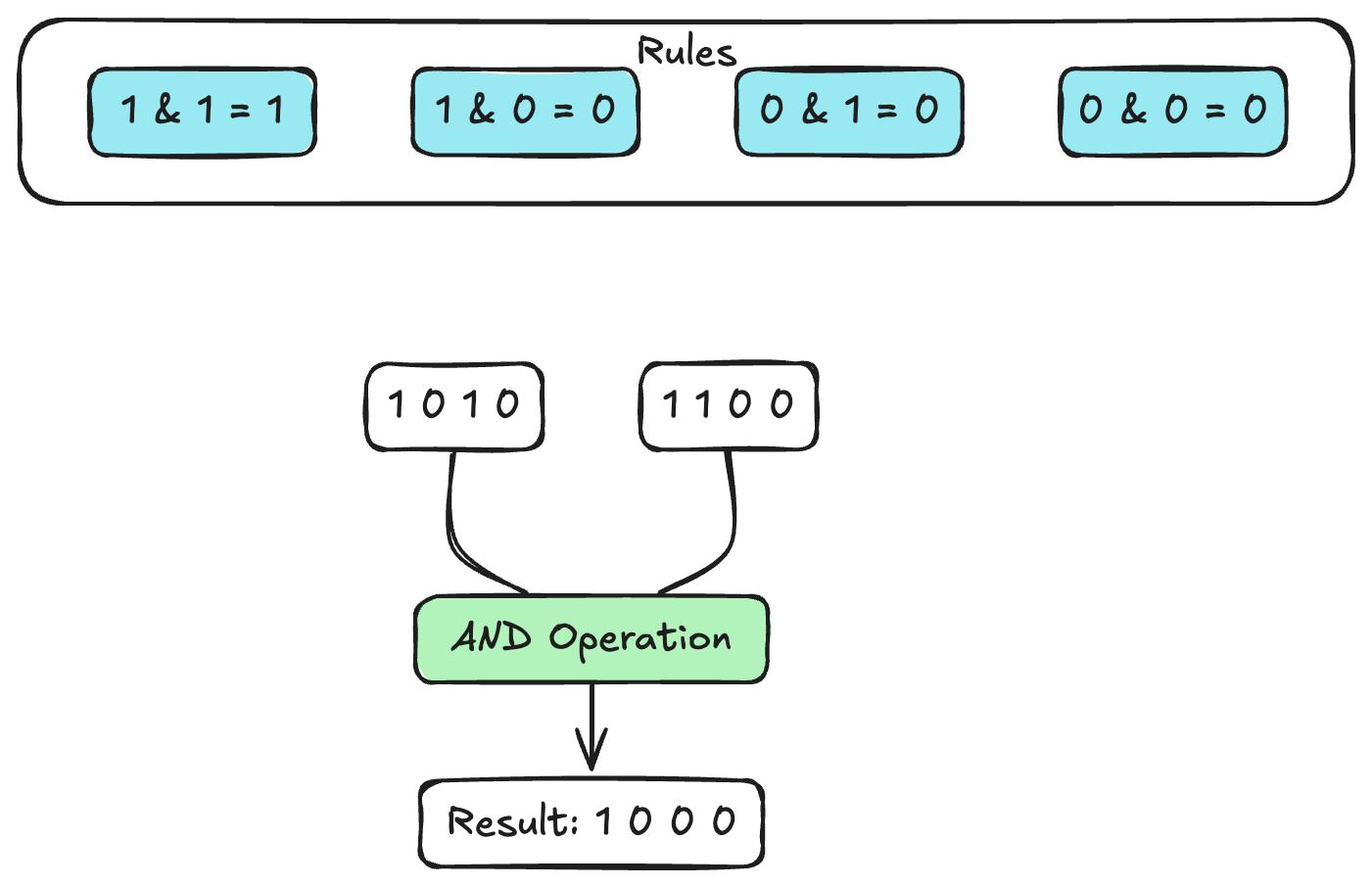
  1 0 1 0  (10)
& 1 1 0 0  (12)
---------
  1 0 0 0  (8)

2. OR (`|`)

The bitwise OR operation performs the logical inclusive OR operation on each pair of bits. The result in each position is 1 if at least one of the bits is 1.

Example:

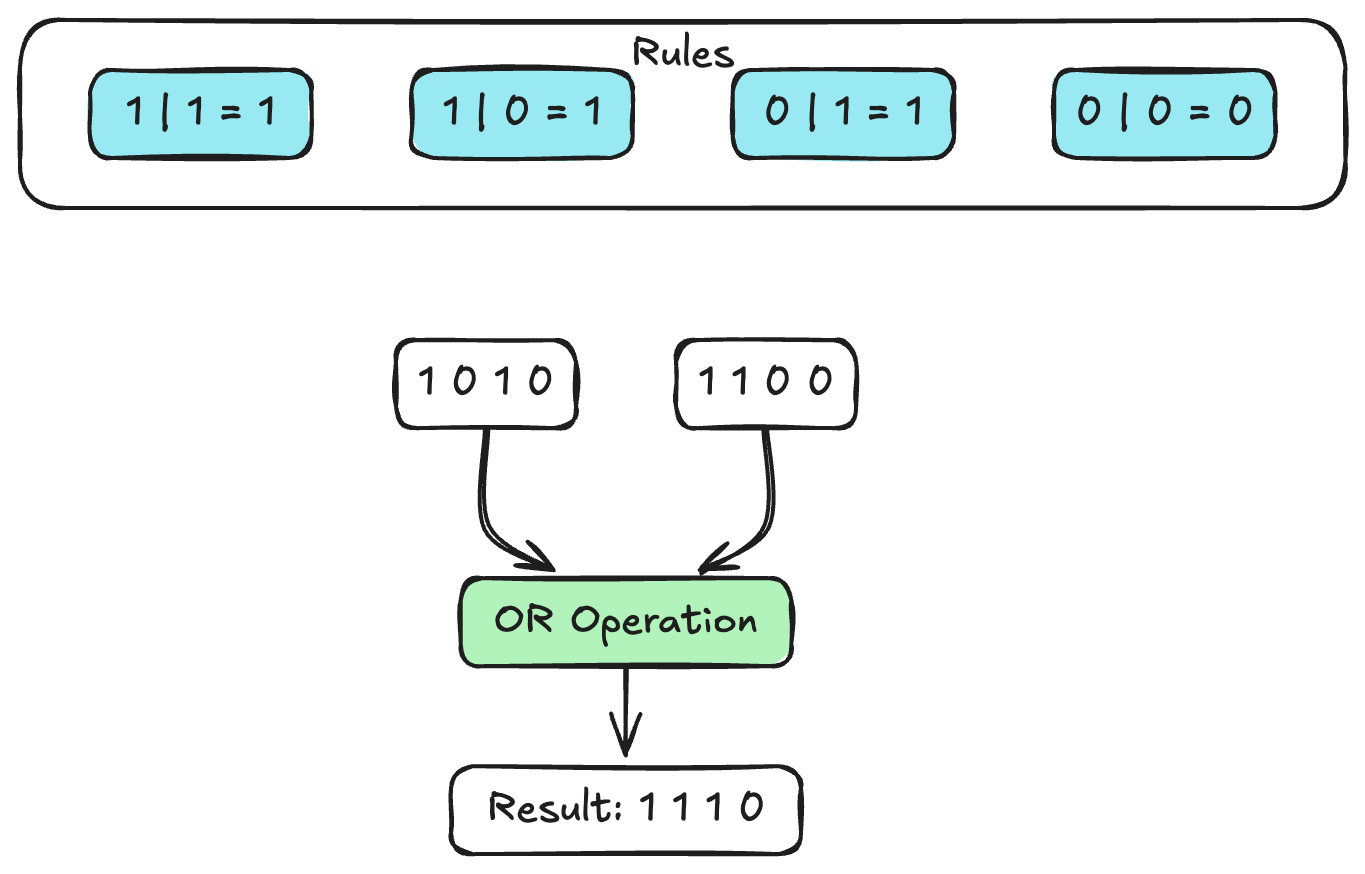
  1 0 1 0  (10)
| 1 1 0 0  (12)
---------
  1 1 1 0  (14)

3. XOR (`^`)

The bitwise XOR (exclusive OR) operation takes two bits and returns 1 if the bits are complementary (i.e., one bit is 1 and the other bit is 0), otherwise it returns 0.

In basic term:

XOR of two different bits (1 and 0) results in 1.
XOR of two identical bits (both 0s or both 1s) results in 0.

Example:

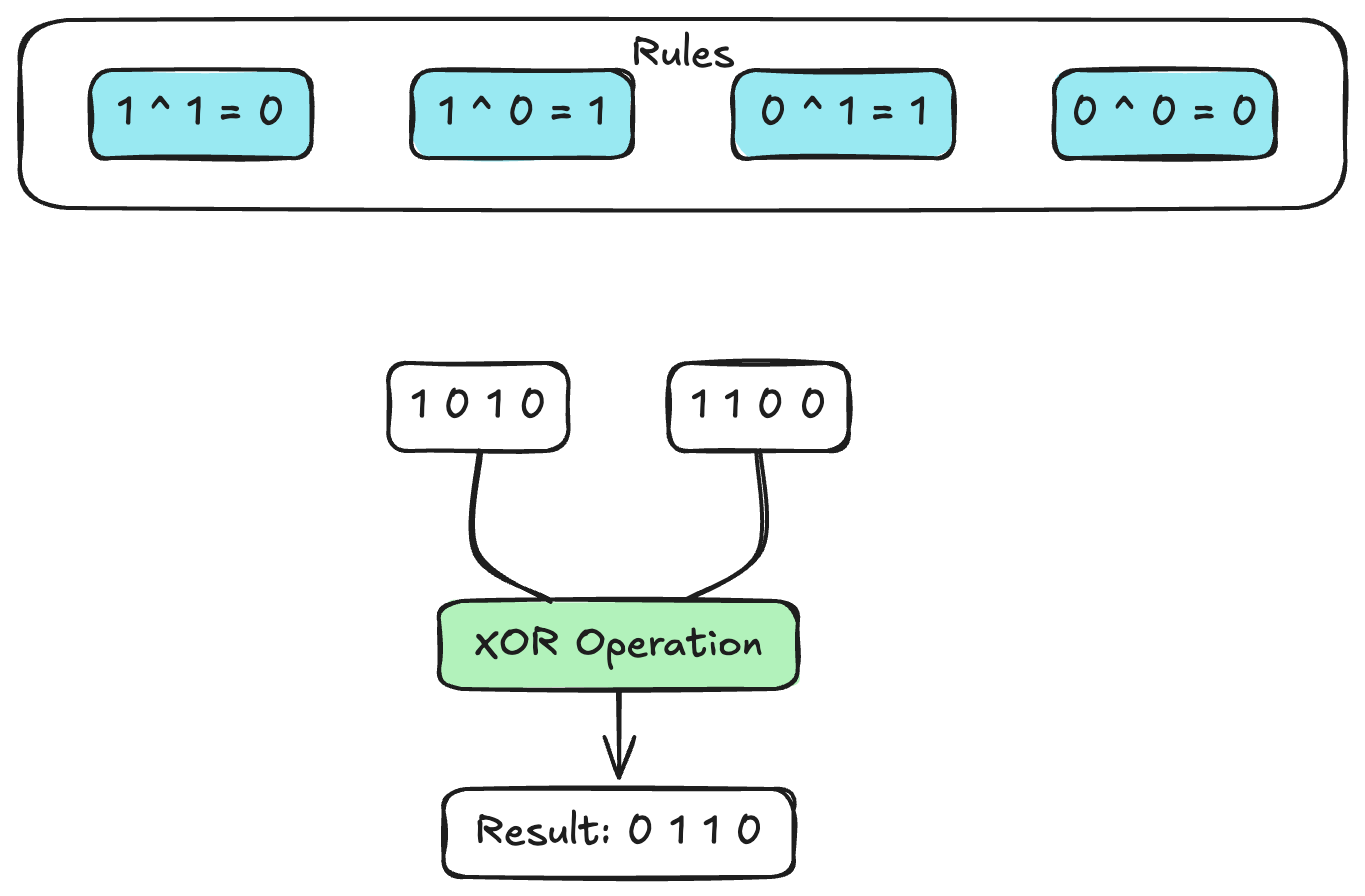
  1 0 1 0  (10)
^ 1 1 0 0  (12)
---------
  0 1 1 0  (6)

4. NOT (`~`)

The bitwise NOT operation, or complement, inverts each bit of a pattern; it transforms each 1 into 0 and each 0 into 1. It's worth noting that Python uses a signed number representation, so the result of a NOT operation might seem surprising at first due to negative number representation (two's complement).

Example:

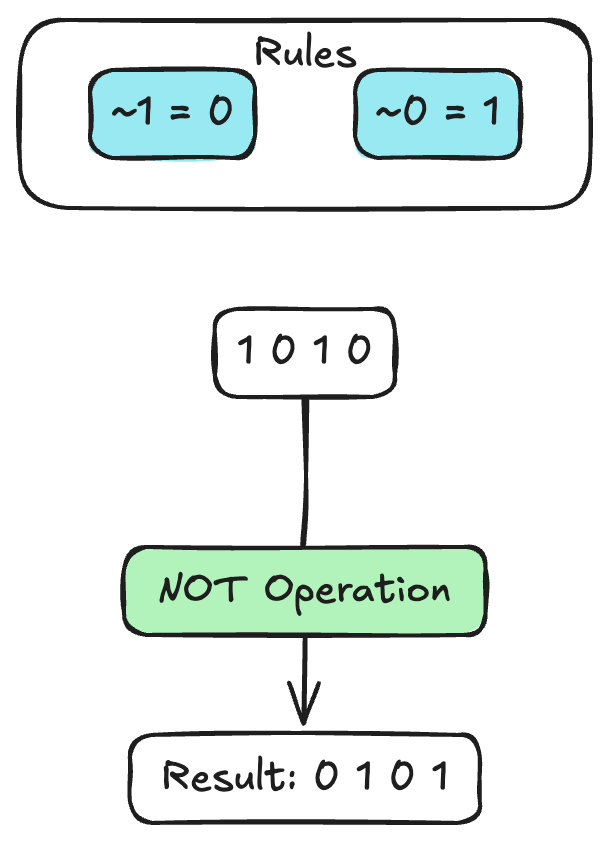
Original:  1 0 1 0
NOT:       0 1 0 1

5. Left Shift (`<<`)

The left shift operation moves all bits in a binary representation to the left by a specified number of places, filling the new rightmost bits with 0s. It's equivalent to multiplying the number by $2^n$ (where n is the number of places to shift).

Example:

5 = 0101
5 << 1 = 1010    (10)
5 << 2 = 10100   (20)
5 << 3 = 101000  (40)
5 << 4 = 1010000 (80)

6. Right Shift (`>>`)

The right shift operation moves all bits in a binary representation to the right by a specified number of places. It's equivalent to floor-dividing the number by $2^n$ .

20 = 10100

20 >> 1 = 01010  (10 in decimal) = 20 ÷ 2¹
20 >> 2 = 00101  (5 in decimal)  = 20 ÷ 2²
20 >> 3 = 00010  (2 in decimal)  = 20 ÷ 2³

Let's take a step backward and think about something interesting:

You know how in most programming languages, we deal with bytes, right? A byte is 8 bits - if we have a value that doesn't need all 8 bits, the language still pads it our to make it a full byte. It's like getting a size 44 shoe for christmas when you're a size 30 - you've got 14 sizes of extra space to deal with. Just like you'd stuff that shoe with extra socks to make it fit and be usable, programming languages automatically pad our smaller values with zeros to fill up the full byte. Whether you like it or not, you're working with the full size either way!

Let's see how this looks at different levels:

High Level (where we usually work):

let x = 5 + 3  // Rust, nice and simple!

Assembly (where things get more "machine-readable"):

mov eax, 5    # Put 5 in the box called eax
add eax, 3    # Add 3 to what's in that box

Machine Code (what the CPU actually deals with):

10111000 00000101  # mov eax, 5
00000011 11000000  # add eax, 3

Now, the CPU is pretty straightforward , it only understands these binary patterns. Think of it like this:

It has circuits that recognize these patterns
When it sees a pattern, it knows exactly what to do
It uses its ALU (like its math brain) to do calculations
At the end of the day, it's all just bits being shuffled around

Assembly language is basically just a human-friendly way to write these binary instructions. It's like having a translator that converts:

Human-readable stuff (assembly)
Into the CPU's native language (binary)

This is why CPU architecture is such a big deal , different CPUs basically speak different "binary dialects", but they're all just pushing bits around in their own way!

Programming use-cases:

1. UNIX File Permission:

A practical example of how UNIX file file permission works.

Let’s define our permission bits:

const READ: u8     = 0b00000100;  // r - Bit 3 is for read
const WRITE: u8    = 0b00000010;  // w - Bit 2 is for read
const EXECUTE: u8  = 0b00000001;  // x - Bit 1 is for execute
const HIDDEN: u8   = 0b00001000;  // h - Bit 4 is for hidden
const SYSTEM: u8   = 0b00010000;  // s - Bit 5 is for system

Before we continue, how will you manipulate this bits using bitwise operations such that you can check when a binary indicates:

all 5 permissions
check write permission
allow read permission
check if write and read are allowed.

Solution:

struct FilePermission {
    flags: u8
}

impl FilePermission {
    // Check if all 5 permissions are set
    fn has_all_permissions(&self) -> bool {
        // 1. Refer to `OR` Bitwise Operation that we discussed earlier.
        let all_perms = READ | WRITE | EXECUTE | HIDDEN | SYSTEM;
        (self.flags & all_perms) == all_perms
    }

    // Check write permission
    fn can_write(&self) -> bool {
        // 2. If the Write Bit is set in flag then we expect the AND operation
        // to not return a Zero. Again Refer to `AND` Bitwise operation
        (self.flags & WRITE) != 0
    }

    // Allow read permission
    fn allow_read(&mut self) {
        self.flags |= READ;
    }

    // Check if both write and read are allowed
    fn can_read_and_write(&self) -> bool {
        let read_write = READ | WRITE;
        (self.flags & read_write) == read_write
    }
}

Let's break down each operation:

Check all permissions:

Current:     XXXXX (our bits)
Required:    11111 (all bits set)
& :          Operation

Must equal  11111 to return true

Check write:

Current:     XXXXX
WRITE mask:  00010
& :          Operation

Must be non-zero to return true, because we expect bit 2 to be set
in current for AND Operation to yield non-zero

Allow read:

Current:     XXXXX
READ:        00001
| :          Operation

Sets read bit regardless of other bits

Check read and write:

Current:     XXXXX
Required:    00011 (READ | WRITE)
& :          Operation

Must equal  00011 to return true

2. Bits Multiplication

Multiply 1 by 2 which in binary is equivalent to: 0001 * 0010

Calculation:

Implementation:

fn main() {
    let a = vec![0_u8, 0, 0, 1];  // 1 in binary
    let b = vec![0_u8, 0, 1, 0];  // 2 in binary
    let mut result: u8 = 0;

    for (i, &bi) in b.iter().enumerate() {
        let mut current: u8 = 0;
        for (j, &ai) in a.iter().enumerate() {
            // Use AND instead of multiplication
            current |= (ai & bi) << j;  // Shift based on position in a
        }
        if i > 0 {
            result |= current << i;     // Shift based on position in b
        } else {
            result = current;
        }
    }
    println!("{}", result);
}

How it works under the hood?

Start with empty result (0000)
Use AND for bit multiplication because:
- 0 & 0 = 0 (same as 0 × 0)
- 1 & 1 = 1 (same as 1 × 1)
- 1 & 0 = 0 (same as 1 × 0)
- 0 & 1 = 0 (same as 0 × 1)
Position management:
- Use shift (<< j) to place each current value in its proper column
- Index 0 result stays at 0
- Index 1 result moves one position left
- And so on...
Combine results:
- Use shift (<< i) to place current result bits in the right position, if you refer to the diagram, you will notice that we are constantly shifting by 1 at each level to preserve previous bits
- Use OR (|=) to accumulate results

3. Volume Control Settings

A simple but practical example of using bit shifts to control volume levels in media systems. By shifting a single bit left or right, we can represent different volume levels in an efficient way.

Let’s define our volume bits:

const MUTE: u8     = 0b0001;
const LOW: u8      = 0b0010;    // MUTE << 1
const MEDIUM: u8   = 0b0100;    // LOW << 1
const HIGH: u8     = 0b1000;    // MEDIUM << 1

Volume Control implementation:

struct Volume {
    level: u8
}

impl Volume {
    fn increase(&mut self) {
        if self.level == 0 || self.level == MUTE {
            self.level = LOW;
        } else {
            self.level <<= 1;  // Shift left to next level
            if self.level > HIGH {
                self.level = HIGH;  // Cap at maximum
            }
        }
    }

    fn decrease(&mut self) {
        if self.level > MUTE {
            self.level >>= 1;  // Shift right to lower level
        }
    }
}

As the volume increases, we shift the bit left:

MUTE:   0001
LOW:    0010  (shifted left once)
MEDIUM: 0100  (shifted left again)
HIGH:   1000  (shifted left again)

Taking a few steps forward...

As you must have know how different number systems represent the same values in various formats (decimal, binary, hexadecimal). Well, there's a fascinating concept here that's worth noting as well.

1. Data Representation Equivalence

Here, the same exact value written in different ways:

let decimal: u8 = 65;
let binary: u8 = 0b01000001;
let hexadecimal: u8 = 0x41;
let ascii_char: char = 'A';

These all represent the exact same bit pattern in memory! , the only difference is just how we look at it. It's like speaking different languages to say the same thing. Here is a link to hexadecimal cheat-set

2. Format Conversion for Manipulation

Sometimes we want to work with our data in different ways. Here's why we might choose each format:

Decimal Format

When we're doing math, decimal numbers just make more sense to our brains:

let ascii_value: u8 = 65;
let new_value = ascii_value + 32;  // Converting 'A' to 'a'

Hexadecimal Format

When we're dealing with colors or byte patterns, hex is super clear:

let color: u32 = 0xFF0000;  // Pure red in RGB

Binary Format

For bit manipulation, nothing beats seeing the actual bits:

let flags: u8 = 0b00000101;  // First and third bits set
let mask: u8 = 0b11110000;  // Upper 4 bits mask

3. Patterns and Formulas

Converting between these formats is pretty straightforward. Example in rust:

use std::num::ParseIntError

// Decimal to Hex
fn decimal_to_hex(decimal: u32) -> String {
    format!("{:#X}", decimal)  // 255 ---> "0xFF"
}

// Hex to Decimal
fn hex_to_decimal(hex_str: &str) -> Result<u32, ParseIntError> {
    u32::from_str_radix(hex_str.trim_start_matches("0x"), 16)  // "0xFF" ---> 255
}

The Big Picture

what's really interesting about all of this is that:

It's all the same data underneath - just different ways of looking at it
We can pick whatever format makes our code clearest
Once we get this, we can be really clever about how we handle data
The computer doesn't care which format we use - it's all binary to it!

This is why computers are so flexible, we can work with data however we want, while the computer just sees bits. Need to do math? Use decimal. Working with colors? Hex is our friend. Messing with flags? Binary's got our back!

Finally , here is how i like to think about it:

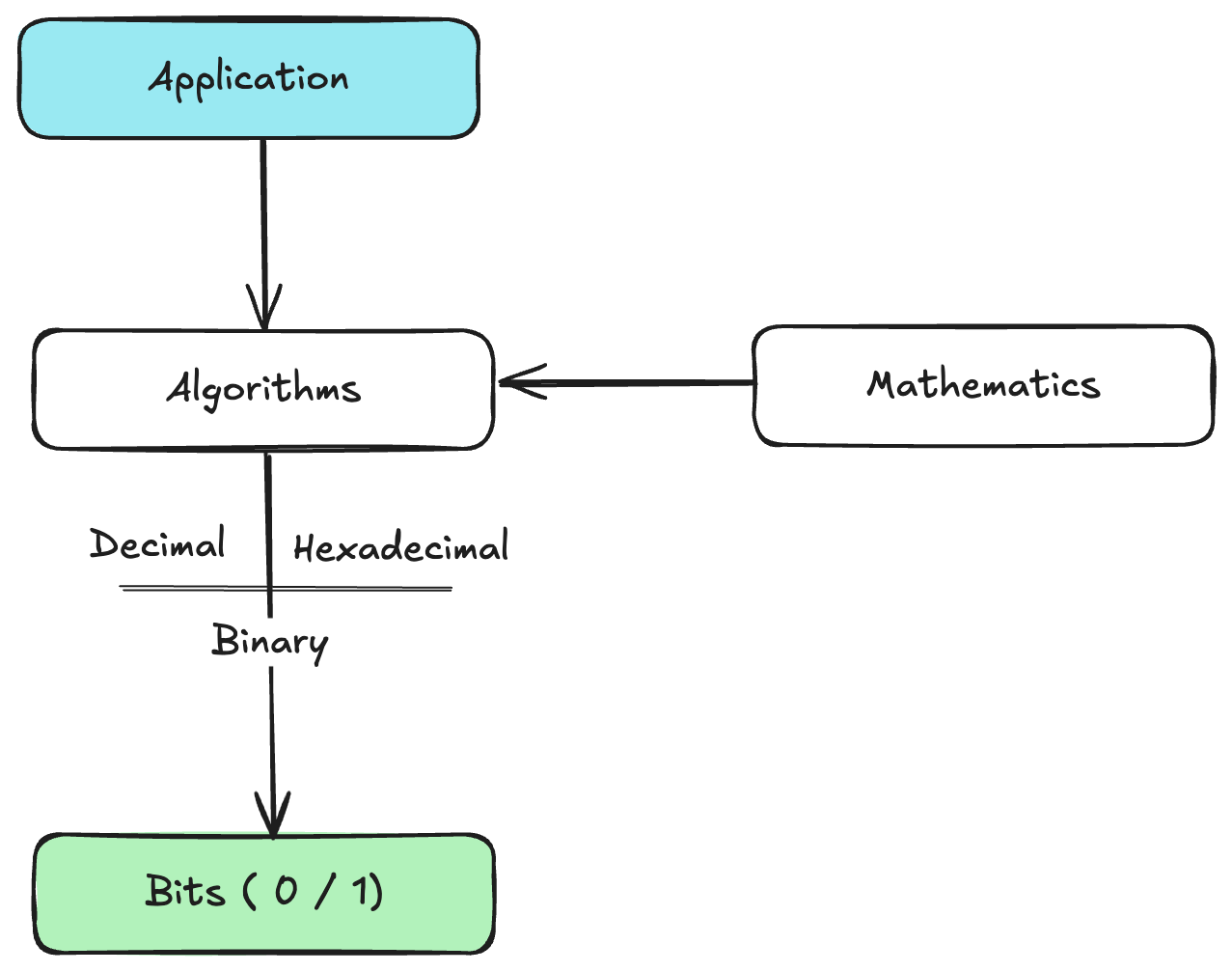
This fundamental concept underlies every advanced computing system we have today. Intelligent systems, encoding/decoding algorithms, cryptography, and even the most novel algorithms , they're all built on these basic principles of data manipulation. What makes computers appear "smart" isn't magic - it's the clever rules and patterns that programmers and scientists have developed to manipulate these bits in increasingly sophisticated ways.

Bits & Bytes: A Guide to Low-Level Bit Manipulation

Introduction

🤔 So... What's The Point?

Bitwise operations

1. AND (&)

Example:

2. OR (|)

Example:

3. XOR (^)

Example:

4. NOT (~)

Example:

5. Left Shift (<<)

6. Right Shift (>>)

Let's take a step backward and think about something interesting:

Let's see how this looks at different levels:

Programming use-cases:

1. UNIX File Permission:

2. Bits Multiplication

3. Volume Control Settings

Taking a few steps forward...

1. Data Representation Equivalence

2. Format Conversion for Manipulation

Decimal Format

Hexadecimal Format

Binary Format

3. Patterns and Formulas

The Big Picture

Finally , here is how i like to think about it:

References

1. AND (`&`)

2. OR (`|`)

3. XOR (`^`)

4. NOT (`~`)

5. Left Shift (`<<`)

6. Right Shift (`>>`)